- Krita Gaussian Noise Reduction Software
- Krita Gaussian Noise Reduction System
- Krita Gaussian Noise Reduction Systems
Auto Brush¶
The generic circle or square. These brush tips are generated by Krita through certain parameters.
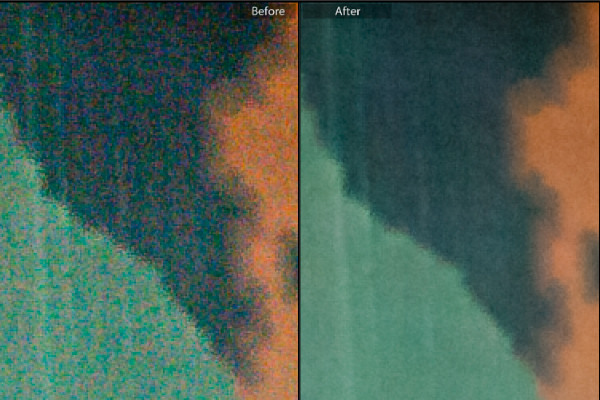
Get The Complete MATLAB Course Bundle for 1 on 1 help! Enroll in the FREE course! (b) Image corrupted image with Gaussian noise with σ =50 (c) Result using 3 3 AWMDF (d) 5 5 AWMDF (e) 7 7 AWMDF (f) 9 9 AWMDF It can be seen that the proposed algorithm performs satisfactorily at various Gaussian noise levels. This can be seen both at the quantitative and qualitative level. For the one above, clone your target picture as a clone layer, and add noise filter mask with 99 level, and 25% opacity. Add a brightness/contrast filter mask. Add a filter layer which is desaturate. Adjust your brightness/contrast filter mask on the clone layer. Krita Gaussian Noise Reduction Line 6 Spider V 120 120w 1x12 Guitar Combo Amp is the best application that runs your apps in a particular space. It prevents your apps from making external changes or other apps and data on your PC. The program can allow you the secure web by running your web browser in the protection layer.
In microscopy, Gaussian noise arises from many sources including electronic components such as detectors and sensors. In addition, salt & pepper noise may al.
Types¶
First, there are three mask-types, with each the circle and square shape:
This is the ultimate generic type. The Fade parameter produces the below results. Of the three auto brushes, this is the fastest.
This one’s fade is controlled by a curve!
This one uses the gaussian algorithm to determine the fade. Out of the three auto brushes, this is the slowest.
Parameters¶
The pixel size of the brush.
Whether the brush is elongated or not.
this sets the softness of the brush. You can click the chain-symbol to lock and unlock these settings. Fade has a different effect per mask-type, so don’t be alarmed if it looks strange, perhaps you have the wrong mask-type.
With fade locked.
With fade separately horizontal and vertical.
This changes the angle a which the brush is at.
This gives the amount of tips related to the ratio.
This determines how much area the brush-covers over its size: It makes it noisy. In the example below, the brush is set with density 0%, 50% and 100% respectively.
This changes the randomness of the density. In the example below, the brush is set with randomness 0%, 50% and 100% respectively.
This affects how far brushes are spaced apart. In the below picture, the three examples on the left are with spacing 0, 1 and 5.
Ticking this will set the brush-spacing to a different (quadratic) algorithm. The result is fine control over the spacing. In the below picture, the three examples on right are with auto spacing, 0, 1 and 5 respectively.
This toggles the super-smooth anti-aliasing. In the below example, both strokes are drawn with a default brush with fade set to 0. On the left without smooth lines, and the right with. Very useful for inking brushes. This option is best used in combination with Auto Spacing.
This changes how smooth the brush is rendered. The lower, the faster the brush, but the worse the rendering looks.You’d want an inking brush to have a precision of 5 at all times, but a big filling brush for painting doesn’t require such precision, and can be easily sped up by setting precision to 1.
This allows you to set the precision linked to the size. The first value is the brush size at which precision is at last 5, and the second is the size-difference at which the precision will decrease.
For example: A brush with ‘’starting brush size’’ 10 and ‘’delta’’ 4, will have…
precision 5 at size 10
precision 4 at size 14
precision 3 at size 18
precision 2 at size 22
precision 1 at sizes above 26.
Predefined Brushes¶
If you have used other applications like GIMP or Photoshop, you will have used this kind of brush. Krita is (mostly) compatible with the brush tip definitions files of these applications:
Gimp autobrush tip definitions.
Gimp single bitmap brush tip. Can be black and white or colored.
Gimp Image Hose brush tip: contains a series of brush tips that are painted randomly or in order after each other. Can be black and white or colored. Krita does not yet support all the parameters yet.
Krita Gaussian Noise Reduction Software
Photoshop brush tip collections. We support many of the features of these brush files, though some advanced features are not supported yet.
Note that the definition of ABR brushes has been reverse engineered since Adobe does not make the specification public. We strongly recommend every Krita user to share brush tips in GBR and GIH format and more complex brushes as Krita presets.
All predefined brush tips are shown in one selector. There are four more options that influence the initial bitmap brush tip you start painting with:
Scales the brush tip. 1.0 is the native size of the brush tip. This can be fairly large! When painting with variable size (for instance governed by pressure), this is the base for the calculations.
Krita Gaussian Noise Reduction System
Initial rotation of the brush tip.
Distance between the brush tip impressions.
Brush Mode¶
For colored brushes, don’t paint the actual colors, but make a grayscale brush tip that will be colored by your selected foreground/background color. Lighter areas will be interpreted as more transparent.
Use the brush tip image exactly as it is. Especially useful for image stamps.
New in version 4.3: Combines the features of Alpha Mask and Image Stamp modes. Transparency is preserved as it is in Image Stamp mode, but colors or gray tones in the brush are replaced by the foreground color. The Lightness values of the brush tip image (if thinking in HSL mode) are preserved, so dark parts of the image are dark, and bright parts are bright. This allows image stamps where you can choose the color, but preserve highlights and shadows, and can even create an effect of thick paint in a brush stroke by simulating the highlights and shadows caused by the texture of the paint and brush stroke (sometimes called an “impasto” effect).
There are three sliders here, to control the exact feel of the current brush tip in Lightness or Gradient mode:
Krita Gaussian Noise Reduction Systems
This is the lightness level that will be the same as your current foreground color. Higher values than this will be lighter versions of the current foreground color, and lower, darker versions of the current color.
Makes the tip as a whole brighter or darker.
Increase the contrast between dark and light areas in the tip.
New in version 4.4: Use the lightness values of the brush tip image as a map to a gradient. Black maps to the left side of the gradient, and white to the right side of the gradient. The gradient used is the currently selected gradient in the main window, so you can change the gradient quickly and easily while painting. This mode allows image stamps with multiple colors that can be changed (great for flowers or other colorful vegetation), and can allow paint brushes that have multiple colors. Image adjustment sliders for Lightness Map mode can be used for this mode too.
Filter 1: Noise Reduction
In everyday situations, there are always external signals that may interfere with the sounds that the hearing aid user actually wants to hear. This ability to distinguish a single sound in a noisy environment is a major concern for the hearing impaired. For people with hearing loss, background noise degrades speech intelligibility more than for people with normal hearing, because there is less redundancy that allows them to recognize the speech signal. Often the problem lies not only in being able to hear the speech, but in understanding speech signals due to the effects of masking. To adjust for this loss, we developed a noise reduction filter in MATLAB for our hearing aid.
Assumptions
To simplify our project, we assume
1) The filter will reduce noise independent of the level of hearing loss of the user, and
2) That any external signals, or noise, can be modeled by white Gaussian noise.
What is white Gaussian noise?
White Gaussian noise (WGN) has a continuous and uniform frequency spectrum over a specified frequency band and has equal power per Hertz of this band. It consists of all frequencies at equal intensity and has a normal (Gaussian) probability density function. For example, a hiss or the sound of many people talking can be modeled as WGN. Because white Gaussian noise is random, we can generate it in MATLAB using the random number generator function, random.
Procedure
Instead of adding white noise to a speech signal, we were able to obtain and generate several .wav sound files of a main speech signal with various sources of white noise in the background.
We experimented with implementing an FIR filter, but after researching various pre-existing MATLAB commands, we used the command wdencmp,which performs noise reduction/compression using wavelets. It returns a de-noised version of the input signal using wavelet coefficients threshholding. We also utilized the MATLAB command ddencmp.
Advantages of Using Wavelets
Wavelets are nonlinear functions and do not remove noise by low-pass filtering like many traditional methods. Low-pass filtering approaches, which are linear time invariant, can blur the sharp features in a signal and sometimes it is difficult to separate noise from the signal where their Fourier spectra overlap. For wavelets the amplitude, instead of the location of the Fourier spectra, differ from that of the noise. This allows for thresholding of the wavelet coefficients to remove the noise. If a signal has energy concentrated in a small number of wavelet coefficients, their values will be large in comparison to the noise that has its energy spread over a large number of coefficients. These localizing properties of the wavelet transform allow the filtering of noise from a signal to be very effective.While linear methods trade-off suppression of noise for broadening of the signal features, noise reduction using wavelets allows features in the original signal to remain sharp. A problem with wavelet denoising is the lack of shift-invariance, which means the wavelet coefficients do not move by the same amount that that the signal is shifted. Ths can be overcome by averaging the denoising result over all possible shifts of the signal. This works very well and even overcomes pseudo-Gibbs phenomena that is often seen due to lack of shift invariance.